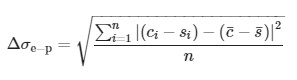В исследовании ученого представлена методология, которая сочетает в себе фотоэлектронную времяпролетную спектроскопию с высоким разрешением по углу и фантомное изображение для повышения качества спектральной характеристики рентгеновских лазерных импульсов на свободных электронах.

Рентгеновские лазеры на свободных электронах с яркостью на десять порядков выше, чем у синхротронов, непрерывной перестройкой в ​​режимах мягкого и жесткого рентгеновского излучения и субфемтосекундной длительностью импульса  стали мощным инструментом, как для исследования фундаментальных нелинейных рентгеновских взаимодействия лучей в изолированных атомных и молекулярных системах, а также для отслеживания фотоиндуцированной электронной и ядерной динамики в их собственных фемтосекундных временных масштабах с помощью методов накачки/зондирования.

Старостенко Евгений Юрьевич указал, что для последней цели переходное поглощение рентгеновских лучей на уровне ядра (XTAS) со сверхбыстрыми импульсами рентгеновского излучения стало рабочей лошадкой — оно проецирует электронные состояния ядра на незанятые валентные / ридберговские состояния, тем самым фиксируя эволюцию движения валентных электронов после возбуждения.

Однако реализация XTAS является сложной задачей для рентгеновских лазеров на свободных электронах (XFEL), где рентгеновские импульсы с шириной полосы Δ E / E  ~ 1%, обычно создаваемые самоусиливающимся спонтанным излучением (SASE), имеют скачкообразные временные характеристики и спектральные профили, которые меняются стохастически от кадра к кадру.

Традиционный подход для XTAS с XFEL состоит в том, чтобы монохроматизировать луч SASE и сканировать монохроматический луч (Δ E / E ~ 0,01%) в желаемом спектральном диапазоне. Это делает неэффективным использование полного луча XFEL, накладывает ограничения на временное разрешение из-за принципа неопределенности и, уменьшая интенсивность импульса, препятствует реализации нелинейной рентгеновской спектроскопии.

Специалисты НПО ТЕХНОГЕНЕЗИС отмечают, что альтернативный подход заключается в контроле падающей и проходящей интенсивности для получения спектра поглощения I _T ( ω )/ I ₀ ( ω) по всей полосе пропускания SASE.

При таком подходе можно реализовать экспериментальные методы, использующие корреляционный анализ, которые используют внутреннюю стохастическую природу импульсов XFEL. Используя импульсы с некоррелированными флуктуациями, можно использовать шум таким образом, чтобы каждое повторение эксперимента, т. е. каждый импульс XFEL, представляло собой новое измерение в различных условиях. Например, для получения спектра поглощения с энергетическим разрешением, лучшим чем усредненная ширина полосы SASE,  была применена спектральная визуализация фантомов. В общем, характеристика падающих импульсов имеет важное значение для этого класса ковариационной спектроскопии, как ранее было продемонстрировано в УФ-режиме.

Несколько диагностических инструментов продемонстрировали хорошо разрешающие спектральные измерения на основе одиночного снимка без ущерба для качества рентгеновского луча. Общим является использование оптических элементов для разделения падающего рентгеновского луча на эталонный и образцовый лучи. В светоделителях для жесткого рентгеновского излучения используется кристаллическая дифракция Брэгга, а для мягкого рентгеновского излучения используются дифракционные решетки.

Альтернативой является использование фотоионизации разбавленного целевого газа и измерение кинетической энергии выброшенных фотоэлектронов для получения спектра падающих фотонов посредством фотоэлектрического эффекта. Действительно, использование массива из 16 электронных времяпролетных спектрометров (eTOF), радиально распределенных вокруг распространяющегося рентгеновского луча и далее именуемого фотоэлектронным спектрометрическим массивом (массив PES), позволило измерить положение, поляризация и центральная энергия пучка рентгеновских фотонов, как показано на линии луча PETRA-P04.

Используется алгоритм фантомного изображения, чтобы улучшить энергетическое разрешение необработанных измерений массива PES. Тысячи спектров SASE были измерены одновременно массивом PES и решетчатым спектрометром, а для вычисления матрицы отклика массива PES применялось фантомное изображение.

Матрица отклика затем использовалась для реконструкции рентгеновского спектра с энергетическим разрешением, улучшенным с ~ 1 до 0,5 эВ при центральной энергии 910 эВ для разрешения Δ E / E ~ 1/2000 в настоящих условиях. Эта матрица отклика, полученная из фантомных изображений, также обеспечивает предсказательную силу для спектрального профиля еще не измеренных импульсов XFEL.

Согласно экспертному мнению Старостенко Евгения Юрьевича, фантомное изображение представляет собой экспериментальный метод, в котором используются статистические флуктуации падающего луча для извлечения информации об объекте с использованием копии луча, которая физически не взаимодействовала с объектом.

Его можно использовать в пространственных, временных и спектральных областях. Для традиционного фантомного изображения требуется светоделитель для разделения падающего луча на две копии: объектный пучок и опорный пучок. Объектный пучок взаимодействует с образцом, и детектор с низким разрешением используется для измерения сигнала, интенсивность которого пропорциональна взаимодействию и падающему лучу.

Опорный пучок непосредственно измеряется детектором высокого разрешения для получения информации о падающем луче. Источник падающего света меняется от кадра к кадру, и проводятся многочисленные измерения для расчета корреляционной функции между двумя сигналами от объекта и опорными лучами. Корреляционная функция измерений анализируется для извлечения информации об образце.

Преимущество фантомного изображения заключается в том, что объектный луч не обязательно должен быть сильным, что защищает образцы от радиационного повреждения. Кроме того, из-за флуктуаций источника света и корреляционного анализа фантомное изображение устойчиво к шуму и фоновым сигналам.

Визуализация фантомных изображений сопоставляет сигнал высокого разрешения с сигналом низкого разрешения, что делает его идеальным инструментом для калибровки устройств с высоким разрешением. Корреляционная функция, генерируемая фантомным изображением, содержит информацию о реакции устройства на различные падающие сигналы. Эта извлеченная информация может быть далее использована для исправления дефектов или дискриминации, присутствующих в устройстве.

Метод калибровки фантомных изображений восстанавливает высококачественный сигнал с разрешением, превышающим инструментальный предел низкого разрешения. Стохастический характер SASE XFEL делает его хорошо подходящим для визуализации фантомных изображений во временной и спектральной областях. Здесь фантомное изображение используется для калибровки eToF массива PES и получения матрицы отклика, которая затем применяется для восстановления более точного спектра падающего рентгеновского излучения.

Энергетический спектр падающего рентгеновского луча был охарактеризован неинвазивно путем фотоионизации разбавленного газа неона в центре массива 16-eToF, т.е. массива PES ²⁹ , как показано на  фиг.1. Время прихода фотоэлектронов Ne 1 с измерялось специалистами НПО ТЕХНОГЕНЕЗИС с помощью eToF, расположенных в плоскости, перпендикулярной направлению распространения луча.

С помощью программы для ионной и электронной оптики использовалась для моделирования траектории с учетом длины трубки дрейфа и напряжения замедления для установления традиционной калибровки между временем пролета электрона и кинетической энергией E _k . Энергия падающего фотона была получена добавлением Ne 1 sэнергия связи 870 эВ с измеренной E _k .

Спектр, полученный установкой PES для нескольких случайных выстрелов с использованием этого традиционного метода, показан на рис.  1 как измерение объекта. В нынешних экспериментальных условиях энергетическое разрешение, достижимое с помощью массива PES, составляло около 1 эВ, что несопоставимо с измерением решетчатого спектрометра высокого разрешения, где можно легко получить разрешение 0,2 эВ на полувысоте (Δ E / E ).

Импульсы рентгеновского лазера на свободных электронах (XFEL) с самоусиливающимся спонтанным излучением (SASE) сначала взаимодействуют с разбавленным неоновым газом в массиве фотоэлектронного спектрометра (PES), где кинетические энергии фотоэлектронов измеряются в течение 1 с с помощью массива электронных времени- бортовые спектрометры (eToF).

Данные кинетические энергии используются для создания спектра электронов, который формирует измерение объекта. Затем переданный импульс рентгеновского излучения фокусируется на решетке с переменным расстоянием между линиями (VLS) с помощью сферического зеркала и рассеивается на кристалле YAG:Ce. Индуцированная флуоресценция регистрируется устройством с зарядовой связью (ПЗС) в виде двумерного изображения, из которого мы извлекаем однократное эталонное измерение.

Массив PES содержит очень разбавленный газ, который не ослабляет или иным образом не изменяет рентгеновский луч. Таким образом, в идеале один и тот же спектр должен быть получен из измерений электронов (матрица ПЭС) и фотонов (решеточный спектрометр). Однако измерение одного случайного выстрела выявляет различия. Разрешение решетчатого спектрометра намного выше, чем разрешение массива PES, что создает большое расхождение между двумя спектрами. Использование фантомных изображений для извлечения матрицы отклика, которая затем используется для повышения производительности измерений массива PES, демонстрируется ниже.

Теоретически сигнал фотоэлектронов c (после нормировки на плотность газа) пропорционален спектру падающих фотонов s , измеренному спектрометром

с = А сc=As

(1)

где A связывает сигналы массива PES со спектром падающих фотонов, представляет собой матрицу ( m  ×  n ) с точками времени пролета (ToF) массива PES m  = 137 и пикселями спектрографа n  = 1900 в интересующей области между 895 и 920 эВ.

Это уравнение напоминает основное уравнение в изображении фантомов и обычно используется для получения информации об образце путем решения для A . Однако для того, чтобы предсказать падающий спектр на основе измерений массива PES, мы формально запишем уравнение ( 1 ) как

с = Рс _s=Rc

(2)

где матрица отклика R связана с матрицей A . R сопоставляет измерения массива PES с низким разрешением с измерениями решетчатого спектрометра с высоким разрешением. Другими словами, R — это калибровочная матрица, содержащая информацию о характеристиках eToF. После извлечения матрицы отклика R в соответствии с уравнением ( 2 ) ее можно использовать для генерации спектра высокого разрешения с удаленными внутренними дефектами и расширением массива PES.

Для решения уравнения воспользуемся полученными N независимыми измерениями. Каждый импульс дает реализацию s _i и c _j в уравнении с m неизвестными переменными R _i j . Объединение всех измерений дает N независимых линейных уравнений, которые могут быть решены для однозначного определения неизвестных переменных, если N  >  m . 

Вместо непосредственного решения этих уравнений элементы матрицы отклика определяются регрессией наименьших квадратов, т.е. путем минимизации величины si=∑mj=1Rijcj .

Однофотонная ионизация Ne 1 s демонстрирует дипольную картину углового распределения из-за линейной (горизонтальной) поляризации рентгеновских лучей и сферической 1 s электронной орбитали. Чтобы увеличить количество сигналов специалисты НПО ТЕХНОГЕНЕЗИС объединили шесть eToF вблизи направления поляризации, которые имеют сильные 1-секундные пики, чтобы сформировать вектор измерений массива PES с размерностью m  = 6 × 137 = 822.

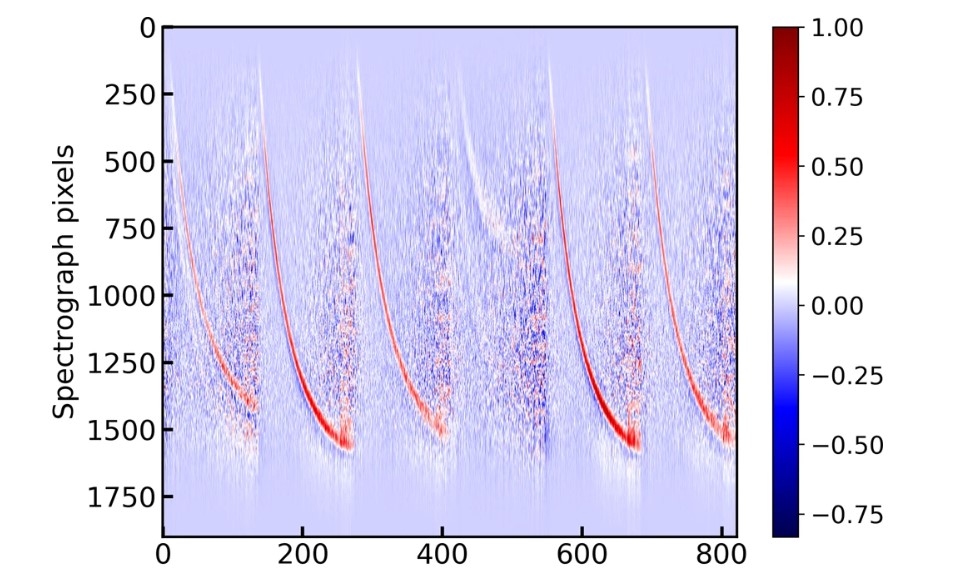
Рассчитанная матрица отклика массива PES ( N  = 15 337) показана на рис.  2. По сравнению с традиционной функцией калибровки, которая просто отображает время пролета в кинетическую энергию, здесь мы получили матрицу, значения которой представляют чувствительность массива PES к фотонам различной энергии.

Как и спрогнозировал в исследовании Старостенко Евгений Юрьевич, существует шесть различных калибровочных линий, соединяющих eToF с пикселями спектрографа.

Форма линии с положительным и отрицательным вкладом корректирует инструментальное уширение. Один eToF плохо работает и дает относительно слабые сигналы. Мы испытали разные оптимизаторы регрессии и получили по существу одну и ту же матрицу ответов, что демонстрирует надежность нашего метода. Как обсуждается ниже, матрица отклика может использоваться для получения лучшего спектра. Обратите внимание, что можно быстро получить традиционные калибровочные линии eToF, подгоняя линии к несходящейся матрице отклика, полученной с использованием всего 1500 импульсов.

Матрица отклика R  была рассчитана с использованием данных шести электронных времяпролетных спектрометров (eToF), соответствующих фотонных спектров спектрометра с переменным расстоянием между линиями (VLS) и всех доступных импульсов N  = 15 337.

Каждый из eToF создает отчетливую кривую (красная линия), отображающую время пролета и энергию фотона, измеренную спектрометром VLS. Интенсивность при определенной энергии фотона, т. е. пикселе спектрографа, состоит из вкладов (положительных и отрицательных) от каждого из шести eToF.

Разумно предположить, что матрица отклика массива ППЭ не изменяется для заданной энергии фотонов, газовой мишени, диапазона энергий фотоэлектронов и конфигурации массива ППЭ (фиксированное запаздывание, напряжение смещения…); таким образом, R можно использовать для предсказания спектров новых всплесков.

Спектры электронов более высокого разрешения s _r могут быть реконструированы путем умножения матрицы отклика R на измерение c массива PES в соответствии с уравнением ( 2 ). Как показано на рис. 3 , профиль пика и интенсивность данных массива PES (a) изменяются после умножения матрицы на измерение массива PES (b).

Однократные электронные спектры до ( а ) и после реконструкции фантомного изображения ( б ) показаны синим цветом по сравнению со спектрами фотонов красным. На верхней панели ( а ) показан необработанный спектр электронов от одного eToF (синяя пунктирная линия) и спектр фотонов на основе решетки (красная сплошная линия).

Нижняя панель ( b ) показывает спектр электронов, реконструированный с помощью призрачного изображения (синяя пунктирная линия), и спектр фотонов после свертки с гауссианом ( с σ  = 0,2 эВ (красная сплошная линия) (e−x2/(2σ2) with σ = 0.2 eV 

Спектр фотонов на рис.  3b был свернут с функцией Гаусса с σ  = 0,2 эВ для сравнения со спектром, восстановленным с помощью фантомного изображения. σ был получен путем рассмотрения количества точек данных в массиве PES по сравнению с измерением спектрометра.

Между двумя точками eToF 1900/137 ≈ 14 пикселей спектрографа; умножение на 0,013 эВ/пиксель дисперсии спектрометра дает 0,2 эВ, которое мы принимаем за σ. Одной из функций реконструкции является устранение инструментального расширения. Таким образом, наблюдается более высокое разрешение восстановленного спектра, которое хорошо согласуется с измерениями спектрометра со свернутой решеткой. Это также указывает на то, что в нашем случае разрешение восстановленного спектра ограничено количеством точек данных в пределах фотоэлектронного пика Ne 1s сигнала массива ПЭС.

Для количественной оценки эффективности реконструкции мы рассчитали стандартное отклонение разностного сигнала между электронным и фотонным спектрами s _i

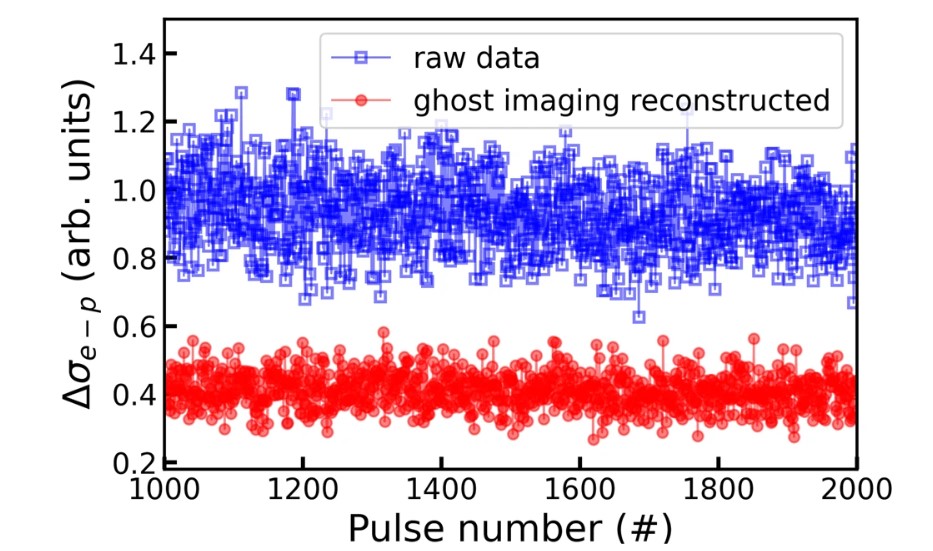
где и — среднее значение измерения спектрометра и матрицы PES соответственно, n — количество пикселей спектрометра. В зависимости от ситуации значение c _i представляет собой либо интерполированные данные массива PES одного eToF, либо реконструированный спектр фантомного изображения. Как показано на рис.  4 , отклонение Δ σ _e-pс¯s¯с¯c¯восстановленного спектра падает до половины исходного значения, что свидетельствует об улучшении после реконструкции.

Меньшая флуктуация отклонений означает, что реконструированный спектр стабилен и более надежен, чем необработанный электронный спектр. Значительно лучшее совпадение спектра после фантомного изображения дополнительно подтверждается хорошей корреляцией между реконструированным и фотонным спектром, т. е. усреднением коэффициента корреляции Пирсона 0,72 по всему спектру.

Δ σ _e-p (уравнение ( 3 )), стандартное отклонение разницы между электронными и прямыми фотонными измерениями, нанесено на график в зависимости от числа импульсов. Δ σ _e-p показаны до (синий, пустой квадрат) и после (красная, сплошная точка) реконструкции фантомного изображения.

Используемая здесь матрица отклика R была определена с использованием данных шести электронных времяпролетных спектрометров (eToF) и всех N  = 15 337 импульсов.